Реферат: Метод экспертных оценок

                                                                                                                   (5.2)

Коэффициенты весов показателей могут быть опреде­лены экспертным путем. Если  -  коэффициент веса h-го показателя, даваемый j-м экспертом, то средний ко­эффициент веса h-го показателя по всем экспертам ра­вен [12]

                                                                                                    (5.3)

Получение групповой экспертной оценки путем сум­мирования индивидуальных оценок с весами компетент­ности и важности показателей при измерении свойств объектов в кардинальных шкалах основывается на пред­положении о выполнении аксиом теории полезности фон Неймана-Моргенштерна как для индивидуальных, так и для групповой оценки и условий неразличимости объектов в групповом отношении, если они неразличимы во всех индивидуальных оценках (частичный принцип Парето). В реальных задачах эти условия, как пра­вило, выполняются, поэтому получение групповой оцен­ки объектов путем суммирования с весами индивидуаль­ных оценок экспертов широко применяется на практике.

Коэффициенты компетентности экспертов можно вы­числить по апостериорным данным, т. е. по результатам оценки объектов. Основной идеей этого вычисления яв­ляется предположение о том, что компетентность экспер­тов должна оцениваться по степени согласованности их оценок с групповой оценкой объектов.

Алгоритм вычисления коэффициентов компетентно­сти экспертов имеет вид рекуррентной процедуры [12]:

                                                                                                   (5.4)

                                                                                                   (5.5)

                                                                                (5.6)

Вычисления начинаются с t=1. В формуле (5.4) началь­ные значения коэффициентов компетентности принима­ются одинаковыми и равными  Тогда по фор­муле (5.4) групповые оценки объектов первого приближе­ния равны средним арифметическим значениям оценок экспертов [12]

                                                                                                         (5.7)

Далее вычисляется величина  по формуле (5.5) [12]:

                                                                                                                    (5.8)

и значение коэффициентов компетентности первого при­ближения по формуле (5.6) [12]:

                                                                                                                   (5.9)

Используя коэффициенты компетентности первого приближения, можно повторить весь процесс вычисле­ния по формулам (5.4), (5.5), (5.6) и получить вторые приближения величин

Повторение рекуррентной процедуры вычислений оце­нок объектов и коэффициентов компетентности естест­венно ставит вопрос о ее сходимости. Для рассмотрения этого вопроса исключим из уравнений (5.4), (5.6) пере­менные  и  и представим эти уравнения в вектор­ной форме [12]

                                                                              (5.10)

где матрицы  В  размерности  и С  размерности  равны [12]

                                                                                               (5.11)

Величина  в уравнениях (5.10) определяется по фор­муле (5.5).

Если матрицы  В и С неотрицательны и неразложи­мы, то, как это следует из теоремы Перрона – Фробениуса, при  векторы  и  - сходятся к собственным векторам матриц В и С, соответствующим макси­мальным собственным числам этих матриц [12]

                                                                                                          (5.12)

Предельные значения векторов х и k можно вычислить из уравнений [12]:

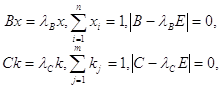                                                                                      (5.13)

где  максимальные собственные числа матриц  В  и С.

Условие неотрицательности матриц  В  и С легко вы­полняется выбором неотрицательных элементов  мат­рицы Х оценок объектов экспертами.

Условие неразложимости матриц В и С практически выполняется, поскольку, если эти матрицы разложимы, то это означает, что эксперты и объекты распадаются на независимые группы. При этом каждая группа экс­пертов оценивает только объекты своей группы. Естест­венно, что получать групповую оценку в этом случае нет смысла. Таким образом, условия неотрицательности и неразложимости матриц  В  и С, а следовательно, и условия сходимости процедур (5.4), (5.5), (5.6) в практи­ческих условиях выполняются.

Следует заметить, что практическое вычисление век­торов групповой оценки объектов и коэффициентов ком­петентности проще выполнять по рекуррентным форму­лам (5.4), (5.5), (5.6). Определение предельных значе­ний этих векторов по уравнению (5.13) требует примене­ния вычислительной техники.

Рассмотрим теперь случай, когда эксперты произво­дят оценку множества объектов методом ранжирования так, что величины  есть ранги. Обработка результа­тов ранжирования заключается в построении обобщен­ной ранжировки. Для построения такой ранжировки введем конечномерное дискретное пространство ранжи­ровок и метрику в этом пространстве. Каждая ранжи­ровка множества объектов j-м экспертом есть точка  в пространстве ранжировок.

Ранжировку  можно представить в виде матрицы парных сравнений, элементы которой определим следу­ющим образом [12]:

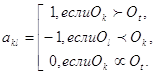
Очевидно, что , поскольку каждый объект эквива­лентен самому себе. Элементы матрицы  антисим­метричны .

Если все ранжируемые объекты эквивалентны, то все элементы матрицы парных сравнений равны нулю. Та­кую матрицу будем обозначать  и считать, что точка в пространстве ранжировок, соответствующая матрице , является началом отсчета.

Обращение порядка ранжируемых объектов приводит к транспонированию матрицы парных сравнений.

Метрика  как расстояние между i-й и j-й ранжировками определяется единственным образом фор­мулой [12]

если выполнены следующие 6 аксиом [12]:

   1.  причем равенство достигается, если ранжировки  и  тождественны;

   2.

   3.

причем равенство достигается, если ранжировка «лежит между» ранжировками  и . Понятие «лежит между» означает, что суждение о некоторой паре  объектов в ранжировке совпадает с суждением об этой паре либо в , либо в  или же в   в   а в  

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10