RSS    

Курсовая работа: Программа для решения квадратных уравнений второго порядка

Квадратное уравнение — уравнение вида ax2 + bx + c= 0, где а не равно нулю.

Получение формулы для решения

Формулу можно получить следующим образом:

аx2 + bx + c = 0

аx2 + bx = − c

Умножаем каждую часть на 4a и прибавляем b2:

4a2x2 + 4abx + b2 = − 4ac + b2

(2ax + b)2 = − 4ac + b2

2ax + b = \pm\sqrt{-4ac + b^2}

Уравнение с вещественными коэффициентами

Квадратное уравнение с вещественными коэффициентами a,~b,~c может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта D = b2 − 4ac:

при D > 0 корней два, и они вычисляются по формуле

x_{1,2} = \frac{-b \pm \sqrt{b^2-4ac}}{2a}; (2.1)

при D = 0 корень один (в некоторых контекстах говорят также о двух равных или совпадающих корнях), кратности 2:

x = \frac{-b}{2a}; (2.2)

при D <0 вещественных корней нет. Существуют два комплексных корня, выражающиеся той же формулой (1) (без использования извлечения корня из отрицательного числа)

Другие записи решений

Вместо формулы (2.1) для нахождения корней можно использовать эквивалентное выражение

x_{1,2} = \frac{-k \pm \sqrt{k^2-ac}}a, (2.3)

где k = b / 2

Это выражение является более удобным для практических вычислений при чётном b, то есть для уравнений вида ax2 + 2kx + c = 0.

Приведённое квадратное уравнение

Квадратное уравнение вида x2 + px + q = 0, в котором старший коэффициент a равен единице, называют приведённым. В этом случае формула для корней (2.1) упрощается до

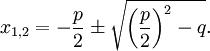x_{1,2}= -\frac p2 \pm \sqrt{\left( \frac p2 \right)^2-q}. (2.4)

Уравнение с комплексными коэффициентами

В комплексном случае квадратное уравнение решается по той же формуле (2.1) и указанным выше ее вариантам, но различимыми являются только два случая: нулевого дискриминанта (один двукратный корень) и ненулевого (два простых корня).

Теорема Виета

Сумма корней приведённого квадратного уравнения x2 + px + q = 0 равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q, то есть

x_1 + x_2 = -p, \qquad\qquad x_1x_2 = q. (2.5)

В общем случае (для неприведённого квадратного уравнения ax2 + bx + c = 0):

x_1 + x_2 = -b/a, \qquad\qquad x_1x_2 = c/a. (2.6)

Разложение квадратного уравнения на множители

Если известны оба корня квадратного уравнения, его можно разложить по формуле

~ax^2+bx+c=a(x-x_1)(x-x_2). (2.7)


В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.

Уравнения, сводящиеся к квадратным

Уравнение вида

a \cdot f^2(x) + b \cdot f(x) + c = 0 (2.8)

является уравнением, сводящимся к квадратному. В общем случае оно решается заменой f(x)=t, t \in E(f) c последующим решением квадратного уравненияa \cdot t^2 + b \cdot t + c = 0.

Также при решении можно обойтись без замены, решив совокупность двух уравнений

f(x) = \frac {-b - \sqrt{b^2-4 \cdot a \cdot c}} {2} (2.9)

f(x) = \frac {-b + \sqrt{b^2-4 \cdot a \cdot c}} {2} (2.10)

Если f(x) = x2, то уравнение принимает вид:

ax4 + bx2 + c = 0

Такое уравнение называется биквадратным

Схе́ма Го́рнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов, при заданном значении переменной. Метод Горнера позволяет найти корни многочлена, а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида x − c. Метод назван в честь Уильяма Джорджа Горнера (англ.).

Описание алгоритма

Задан многочлен P(x):


P(x) = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \ldots + a_n x^n, \quad a_i \in \mathbb{R}.

Пусть требуется вычислить значение данного многочлена при фиксированном значении x = x0. Представим многочлен P(x) в следующем виде:

P(x) = a_0 + x(a_1 + x(a_2 + \cdots x(a_{n-1} + a_n x) \dots)).

Определим следующую последовательность:

b_n = a_n\,\!

b_{n-1} = a_{n-1} + b_n x\,\!

b_i = a_i + b_{i+1} x\,\!

b_0 = a_0 + b_1 x\,\!

Искомое значение P(x0) = b0. Покажем, что это так.

В полученную форму записи P(x) подставим x = x0 и будем вычислять значение выражения, начиная со внутренних скобок. Для этого будем заменять подвыражения через bi:

\begin{align}P(x_0) &amp; = a_0 + x_0(a_1 + x_0(a_2 + \cdots x_0(a_{n-1} + a_n x_0)\dots)) \\&amp; = a_0 + x_0(a_1 + x_0(a_2 + \cdots x_0(b_{n-1})\dots)) \\&amp; {} \ \ \vdots \\&amp; = a_0 + x_0(b_1) \\&amp; = b_0\end{align}

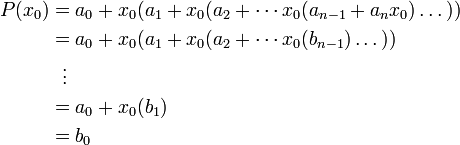
Использование схемы Горнера для деления многочлена на бином

При делении многочлена a_0 x^n + a_1 x^{n-1} + \cdots + a_{n-1} x + a_n на x − c получается многочлен b_0 x^{n-1} + b_1 x^{n-2} + \cdots + b_{n-2} x + b_{n-1} с остатком bn.

3. Проектирование

программа интерфейс нелинейное уравнение

3.1 Требования к аппаратному обеспечению

При выборе персонального компьютера, необходимо чтобы он обладал такими характеристиками как надежность, разрядность, производительность (тактовая частота), емкость основной памяти, емкость жесткого диска, тип принтера, вид операционной системы, поддержка сети, совместимость с другими компьютерами. Очень важно выбрать монитор, потому что от него зависит комфортность работы и здоровье пользователя. При выборе монитора необходимо учесть следующие факторы: размер экрана, размер зерна экрана, разрешающая способность, частота кадровой развертки, объем памяти видеоадаптера.

Экран желательно иметь плоский, антибликовый, с антистатическим покрытием (типа AS- Anti Static), с низким уровнем излучения (тип- LR- Low Radiation). При выборе принтера нужно учесть: цветность, тип принтера (матричный, струйный, лазерный), количество игл или сопел, ширину печати, разрешающую способность, скорость печати, русификацию, емкость памяти, интерфейс, расходные материалы.

Для работы программы необходимо следующее минимальное аппаратное и программное обеспечение:

- Процессор Pentium III 400 Мгц или аналогичный:

- 128 Мб оперативной памяти;

- 24 Мб свободного места на диске ;

- клавиатура;

- ручной манипулятор «мышь»;

- видео карта 32 Мб;

- 48-скоростной дисковод CD-ROM;

- операционная система MS Windows версий от Windows 98;

- пакет программ Microsoft Office.

- среда программирования Borland Delphi 6

Эти требования являются минимальными, что означает, что при повышении класса компьютера и увеличении его производительности, эффективность использования программы также повысится.

Cостав ПК, на котором тестировалась программа

- Процессор AMD Athlon 1300, 1.30 Ггц

- 512 Мб оперативной памяти;

- 100 Гб свободного места на диске ;

- клавиатура;

- ручной манипулятор «мышь»;

- видео карта GeForce 4, 64 Мб;

- 52-скоростной дисковод CD-ROM;

- операционная система MS Windows XP;

- среда программирования Borland Delphi 7

3.2 Инструкция пользователя

Данный программный продукт должен реализовывать следующие основные возможности:

- решение уравнения с помощью дискриминанта;

- решение уравнения теоремой Виетта;

- решение квадратного уравнения с помощью таблицы Горнера;

В результате разработки данного программного средства получилась выходная документация: инструкция пользователя и инструкция программиста.

Выполнение программы.

Для начала работы с программой следует загрузить на диск С: файлы программы в одну папку с CD, содержащим программу.

Для запуска программы следует запустить файл Project1.exe.

Появится главное окно программы в соответствии с рисунком 3.1


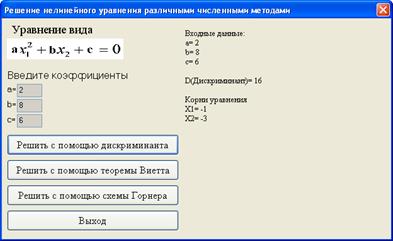
Рисунок 3.1 – Главное окно программы

В правой части окна расположено поле вывода данных. В левой же части вводятся данные и находятся кнопки управления программой.

Кнопки управления следующие:

- «Решить с помощью дискриминанта» - решение квадратного уравнения стандартным методом (с помощью нахождения дискриминанта);

- «Решить с помощью теоремы Виетта» - нахождение решения с применением теоремы Виетта;

Страницы: 1, 2, 3, 4

Новости


Быстрый поиск

Группа вКонтакте: новости

Пока нет

Новости в Twitter и Facebook

                 

Новости

Обратная связь

Поиск
Обратная связь
Реклама и размещение статей на сайте
© 2010.