Реферат: Организация математических операций в С++
Виртуальные функции
Виртуальные функции определяются в родительском классе, а в производных классах происходит доопределение этих функций и для них создаются новые реализации. При работе с виртуальными функциями сообщения передаются как указатели, которые указывают на объект вместо прямой передачи объекту. Виртуальные функции используют таблицу для адресной информации. Эта таблица инициализируется во время выполнения при помощи конструктора.
Конструктор вызывается каждый раз, когда создается объект его класса. Задача конструктора в данном случае состоит в связывании виртуальной функции с таблицей адресной информации. Во время компиляции адрес виртуальной функции неизвестен; вместо этого ей отводится позиция в таблице адресов. Эта позиция будет содержать адрес функции [5].
Глава 2. Задачи линейной алгебры
2.1. Вычисление определителей
Пусть имеем квадратную матрицу размером n´n:
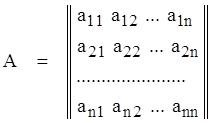. (2.1.1)
Требуется вычислить определитель матрицы det(A).
Эквивалентным преобразованием матрицы называют преобразования матрицы, не изменяющие величину определителя матрицы. Эквивалентным является следующее преобразование: любую строку матрицы можно заме-нить суммой исходной строки и любой другой, умноженной на любое число, не равное нулю.
Используя такого рода преобразования можно попытаться привести ис-ходную матрицу к треугольному виду:
,
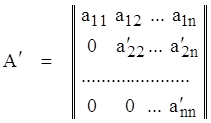при этом det(A) = det(A¢).
Формула для пересчета элементов матрицы имеет вид:
,
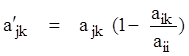(2.1.2)
где i - номер столбца, в котором элементы, лежащие ниже
главной
диагонали,
превращаются в нули;
j - номер элемента в обрабатываемом столбце (т.е. номер строки);
k - номер элемента в текущей строке.
Алгоритм приведения матрицы к треугольному виду включает в себя 3 вложенных цикла:
- внешний цикл, i = 1 .. n-1 ;
- средний цикл, j = i+1 .. n ;
- внутренний цикл, k = i+1 .. n .
Теперь искомый определитель вычисляется как произведение диагональ-ных элементов:
.
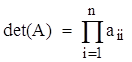Описанный выше алгоритм дает результат не всегда. Если при выполне-нии i-того шага внешнего цикла диагональный элемент aii оказывается рав-ным нулю, а среди элементов i-того столбца с номерами от i+1 до n есть хотя бы один не нулевой, алгоритм завершается безрезультатно (из-за невозмож-ности вычислений по формуле (2.1.2). Для того, чтобы это не происходило, используется прием, который называется «выбор главного элемента».
При выполнении очередного шага цикла по i предварительно выполняют-ся следующие операции:
1) находится максимальный по модулю элемент среди элементов i-то-го столбца от aii до ani ;
2) если найденный элемент ali равен нулю, процесс вычисления завер-шается с выдачей результата det(A) = 0 ;
3) если l¹i , тогда строки исходной матрицы с номерами i,l поменять местами.
После завершения преобразования матрицы, определитель вычисляется по формуле:
,
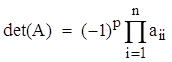где p – число выполненных операций перемены строк местами.
2.2 Обращение матриц
Обратной к матрице A называется матрица A-1, обладающая свойством:
A×A-1 = A-1×A = I ,
где I – единичная диагональная матрица. Опишем один из универсальных и эффективных методов расчета обратной матрицы (метод Жордана-Гаусса, в книге [4-218] описан как «метод исключений»). В [5-22] приведен более эф-фективный по памяти алгоритм обращения матрицы.
Пусть имеем матрицу A вида (2.1.1) и пусть B – единичная диагональная матрица такого же размера. Создадим рабочую матрицу R размером N´2N просто присоединив матрицу B справа к матрице A :
.
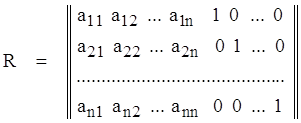Над строками такой расширенной матрицы будем производить преобра-зования, аналогичные тем, которые были описаны в п.2.1. Левую часть мат-рицы R будем называть подматрицей A, правую – подматрицей B. Весь про-цесс преобразования матрицы R разобьем на 3 этапа.
1 этап. Выполним преобразования строк матрицы так, чтобы все элемен-ты, лежащие ниже диагональных элементов подматрицы A, обратились в ну-ли. При этом может использоваться выбор главного элемента.
2 этап. Выполним преобразования так, чтобы все элементы, лежащие вы-ше диагональных элементов подматрицы A, обратились в нули. Преобразо-вания надо выполнять в обратном порядке: со столбца номер n и до столбца номер 2.
3 этап. Каждую строку расширенной матрицы R с номером i делим на ди-агональный элемент aii .
После завершения процедуры подматрица A превращается в единичную диагональную матрицу, а подматрица B будет равна искомой обратной мат-рице A-1 . Алгоритм имеет порядок O(n3).
2.3. Методы решения систем линейных уравнений
Задача поиска решений системы линейных уравнений имеет не только са-мостоятельное значение, но часто является составной частью алгоритма ре-шения многих нелинейных задач. Основные методы решения СЛУ:
- метод Гаусса;
- метод обращения матрицы;
- итерационные методы.
2.4. Метод Гаусса
Пусть имеем систему линейных уравнений:
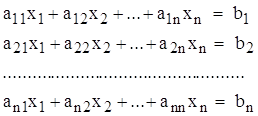
Простой метод Гаусса состоит в следующем.
Составим расширенную матрицу, приписав к матрице коэффициентов СЛУ дополнительный столбец – правые части уравнения:
.
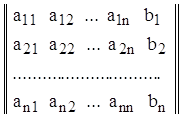Выполним над строками расширенной матрицы преобразования, анало-гичные тем, которые были описаны в п. 2.1:
,
,
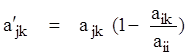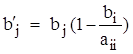и приведем ее к треугольному виду:
.
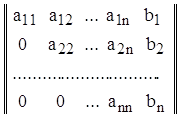Теперь можно вычислить искомые величины xi , начиная с последнего, т.е. вначале находится xn , затем xn-1, xn-2, … , x1. Формула для вычислений имеет вид:
.
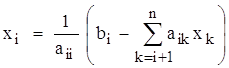Для расширения возможностей и повышения устойчивости приведенного алгоритма используется выбор главного элемента. Порядок метода Гаусса равен O(n3).
2.5. Метод обращения матрицы
Представим систему линейных уравнений в матричной форме:
.
Умножим последнее равенство слева на A-1 :
.
Учитывая, что A-1×A = I , формально получаем искомое решение:
Таким образом, решение системы выполняется в два этапа:
1) вычисление обратной матрицы;
2) умножение обратной матрицы на вектор правых частей СЛУ.
Несмотря на то, что метод обращения матрицы имеет такой же порядок, как и метод Гаусса - O(n3), по объему вычислений он проигрывает ему в нес-колько раз. Однако, если СЛУ необходимо решать многократно и при этом изменяется лишь вектор правых частей, метод обращения матрицы становит-ся все же выгодным.
Практическая часть
Описание класса Matrix для решения задач линейной алгебры
Класс имеет приватные и общедоступные члены-данные и члены-функции (методы). Для хранения компонентов матрицы используется одномерный динамический массив элементов типа параметра шаблона. Для создания объекта предусмотрены три конструктора: конструктор по умолчанию, конструктор с параметрами, конструктор копирования и деструктор. Для выполнения множества матричных операций созданы перегруженные операции: присваивания (=), сложения (+), вычитания (-), умножения(*) и т.п. На базе операторов ввода/вывода С++ разработаны функции ввода матриц из потока и вывода их в поток, предусматривающие в случае файлового ввода/вывода как текстовую форму хранения, так и бинарную.
Доступ к членам-данным класса – числу строк и столбцов матрицы осуществляется с помощью методов size_row( ) и size_col( ). Для доступа к элементам матрицы создан перегруженный оператор вызова функции operator( ) (dim x, dim x), где dim – переопределенный тип unsigned char. Вызов функции используется как оператор индексирования, принимающий два аргумента. Аналогично создан оператор вызова функции с одним аргументом operator( ) (dim x). Для данного класса – это очень важные перегруженные операторы, т.к. они используются во всех функциях и операторах, в которых происходит обращение к элементам матрицы.
Описание функций, конструкторов и деструкторов класса:
