Реферат: Прикладная математика
Таблица 6
|
|
x - x4 |
0 100 200 300 400 500 600 700 |
| x4 |
F3(x - x4) f4(x4) |
0 25 45 63 79 94 112 126 |
| 0 | 0 | 126 |
| 100 | 30 | 142 |
| 200 | 52 | 146 |
| 300 | 76 | 155* |
| 400 | 90 | 153 |
| 500 | 104 | 149 |
| 600 | 116 | 141 |
| 700 | 125 | 125 . |
§9. Динамическая задача управления производством
|
Предприятие производит партиями некоторые изделия. Предположим, что оно получило заказы на n месяцев. Размеры заказов значительно меняются от месяца к месяцу. Поэтому иногда лучше выполнять одной партией заказы нескольких месяцев, а затем хранить изделия, пока они не потребуются, чем выполнять заказ в тот именно месяц, когда этот заказ должен быть отправлен. Необходимо составить план производства на указанные n месяцев с учетом затрат на производство и хранение изделий. Обозначим:
xj - число изделий, производимых в j -й месяц;
yj - величина запаса к началу j го месяца (это число не содержит изделий, произведенных в j -м месяце);
dj - число изделий, которые должны быть отгружены в j -й месяц;
fj (xj,yj+1) - затраты на хранение и производство изделий в j -м месяце.
Будем считать, что величины запасов к началу первого месяца y1 и к концу последнего yn+1 заданы.
Задача состоит в том, чтобы найти план производства
(x1, x2, ..., xn) (1)
компоненты которого удовлетворяют условиям материального баланса
xj + yj
- dj = yj+1 j = 1,n (2)
и минимизируют суммарные затраты за весь планируемый период
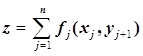(3)
причем по смыслу задачи
xj ³ 0, yj ³ 0, j = 1,n (4)
Прежде чем приступить к решению поставленной задачи, заметим, что для любого месяца j величина yj+1 запаса к концу месяца должна удовлетворять ограничениям
0 £ yj+1 £ dj+1 + dj+2 + ... + dn (5)
т.е. объем производимой продукции xj на этапе j может быть настолько велик, что запас yj+1 удовлетворяет спрос на всех последующих этапах, но не
имеет смысла иметь yj+1 больше суммарного спроса на всех последующих этапах. Кроме того, из соотношений (2) и (4) непосредственно следует, что переменная xj должна удовлетворять ограничениям
0 £ xj £ dj + yj+1 (6)
Следует также заметить, что переменные xj, yj могут принимать только целые неотрицательные значения, т.е. мы получили задачу целочисленного нелинейного программирования.
Будем решать задачу (1)-(6) методом динамического программирования.
Введем параметр состояния и составим функцию состояния.
|
x = yk+1 (7)
а функцию состояния Fk(x) определим как минимальные затраты за первые k месяцев при выполнении условия (5)
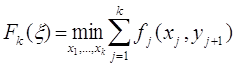(8)
где минимум берется по неотрицательным целым значениям x1,...,xk, удовлетворяющим условиям
xj + yj
- dj = yj+1 j = 1, k-1
(9)
xk + yk - dk = x (10)
Учитывая, что
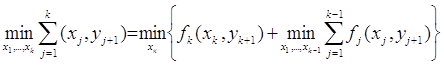(11)
и величина запаса yk к концу (k-1) периода, как видно из уравнения (10), равна
yk = x + dk - xk (12)
приходим к рекуррентному соотношению
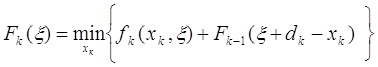(13)
где минимум берется по единственной переменной xk, которая, согласно (6) может изменяться в пределах
0 £ xk £ dk + x (14)
принимая целые значения, причем верхняя граница зависит от значений параметра состояния, изменяющегося в пределах
0 £ x £ dk+1 + dk+2 + ... + dn (15)
а индекс k может принимать значения
k = 2, 3, 4, ... , n (16)
Если k=1, то
F1(x = y2) = min f1(x1, x) (17)
x1
где
x1 = x + d1 - y1 (18)
0£ x £ d2 + d3 + ... + dn (19)
|
Применив известную вычислительную процедуру динамического программирования, на последнем шаге (при k = n) находим значение последней компоненты xn* оптимального решения, а остальные компоненты определяем как
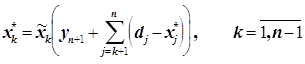(20)
Рассмотрим более подробно функции затрат fj(xj, yj+1) и рекуррентные соотношения. Пусть
jj(xj) = axj2 + bxj + c
jj (xj) - затраты на производство (закупку) xj единиц продукции на этапе j;
hj - затраты на хранение единицы запаса, переходящей из этапа j в этап j+1.
Тогда затраты на производство и хранение на этапе j равны
fj(xj, yj+1) = jj(xj) + hj yj+1 = axj2 + bxj + c + hj yj+1. (21)
Выведенные ранее рекуррентные соотношения динамического программирования для решения задачи управления производством и запасами в нашем случае принимают вид:
(22)
где
k = 2, 3, ... , n (23)
0 £ yk+1 £ dk+1 + dk+1 + ... + dn (24)
0 £ xk £ dk + yk+1 (25)
yk = yk+1 + dk - xk (26)
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 |
