 Реферат: Распределенные алгоритмы
Реферат: Распределенные алгоритмы
Асинхронная обработка уведомлений. Было этой части предположили что уведомления о топологических изменениях обрабатываются автоматически вместе с именением в единой транзакции. Обработка происходит на обоих сторонах удаленного или добавленного канал одновременно. Лампорт [Lam82] выполнил анализ мелких деталей и учел задержки в обработке этих уведомлений. Коммуникационный канал от w до u смоделирован объединением трех очередей.
(1) OQwu , выходная очередь w,
(2) TQwu , очередь сообщений (и пакетов данных) передаваемая
(3) IQwu , входная очередь u.
При нормальном функционировании канала, w посылает сообщение к u добавлением его в OQwu, сообщения двигаются от OQwu к TQwu и от TQwu к IQwu, и u получает их удаляя из IQwu. Когда канал отказывает сообщения в TQwu выбрасываются и сообщения в OQwu соответственно выбрасываются раньше чем добавились к TQwu. Сообщение < fail, w> становится в конец IQwu, и когда нормальное функционирование восстановилось сообщение <repair,w> также становится в конец IQwu. предикаты P(u, w, v) принимают слегка более сложную форму но алгоритм остается тот же самый.
Маршрутизация по кротчайшему пути. Возможно означить вес каждого канала и модифицировать алгоритм так чтобы вычислять кратчайший путь вместо пути с минимальным количеством шагов. Процедура Recompute алгоритма Netchange использовать вес канала uw в вычислении оценки длины кратчайший путь через w если константу 1 заменить на wuw. Константа N в алгоритме должна быть заменена верхней границей диаметра сети.
Довольно просто показать что когда модифицированный алгоритм достигнет стабильной конфигурации таблицы маршрутизации будут корректны и содержать оптимальный путь (все циклы в сети должны иметь положительный вес). Доказательство что алгоритм действительно достигает такого состояния требует более сложной нормфункции.
Даже возможно расширить алгоритм для работы с изменяющимися весами каналов; реакция узла u на изменение веса канала – перевычисление Du[v] для v. Алгоритм был бы практическим, однако, только в ситуации когда среднее время изменений стоимостей каналов больше времени сходимости что не реально. В этих ситуациях должна алгоритм должен предпочесть гарантию свободы от циклов в течение сходимости, на пример алгоритм Мерлина-Сигалла.
4.4 Маршрутизация с Компактными Таблицами маршрутизации
Обсужденные алгоритмы маршрутизации требуют что бы каждый узел содержал таблицу маршрутизации с отдельной ссылкой для каждого возможного пункта назначения. Когда пакет передается через сеть эти таблицы используются каждом узле пути (исключая пункта назначения). В этой части рассматриваются некоторые организации таблиц маршрутизации которые хранение и поиск механизмов маршрутизации. Как эти таблицы маршрутизации могут быть вычислены распределенными алгоритмами здесь не рассматриваются. Для простоты представления положим что сеть связная.
Стратегию уменьшения таблицы в каждом из трех механизмов маршрутизации, обсуждаемых в этой части, просто объяснить следующим образом. Если таблицы маршрутизации узла хранят выходящий канал для каждого пункта назначения отдельно, таблица маршрутизации имеет длину N; следовательно таблицы требуют W(N) бит, не важно как компактно выходящий канал закодирован для каждого пункта назначения. Теперь рассмотрим перестройку таблицы: таблица содержит для каждого канала узла ссылку говорящую какие пункты назначения должны быть смаршрутизированны через этот канал; смотри Рисунок 4.11. Таблица теперь имеет "длину" deg для узел с deg каналами; теперь компактность зависит от того как компактно множество пунктов назначения для каждого канала может быть представлено.
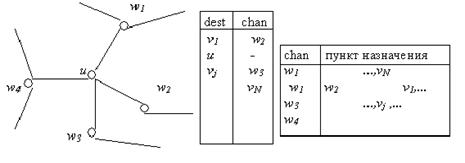
Рисунок 4.11 Уменьшение размера таблицы маршрутизации.
Первый метод компактной маршрутизации был предложен Санторо и Кхатибом [SK85]. Метод основан на пометке узлов целыми от 0 до N— I, таким образом чтобы множество пунктов назначения для каждого канала было интервалом. Пусть ZN обозначает множество {0, 1,..., N- 1}. В этой части все арифметические операции по модулю N, т.e., (N— 1) + 1º 0.
Определение 4.19 Циклический интервал [a, b) в ZN – множество целых определенное как
ì {a, a +1,..., b -1} если a<b
[a,b)= í {0,. . ., b- 1, a,..., N-1} если a³b
î
Заметим что [a, a) = ZN, и для a ¹ b дополнение [a, b) – [b, a). Циклический интервал [a, b) называется линейным если a < b.
Теорема 4.20 Узлы дерева T могут быть пронумерованы таким образом что для каждого выходящего канала каждого узла множество пунктов назначения которые маршрутизируются через данный канал есть циклический интервал.
Доказательство. Возьмем произвольный узел vо за корень дерева и для каждого w пусть обозначим за T[w] поддерево T с корнем в w. Возможно перенумеровать узлы таким образом чтобы для каждого w числа для означивания узлов в T[w] составляли линейный интервал, на пример префиксным обходом дерева как на Рисунке 4.12. В этом порядке, w – первый узел дерева T[w] который посетится и после w все узлы T[w] посетятся перед узлами не входящими в T[w]; следовательно узлы в T[w] перенумерованы линейным интервалом [lw, lw +|T{w]|) (1w метка w).
Через [aw,
bw) обозначим интервал чисел означивающие узлы в T[w]. Сосед
w – один из двух сыновей или отец w. Узел w передает к
сыну u пакеты с пунктом назначения в T[u], т.е., узлы с числами
в [au, bu). Узел w передает своему
отцу пакеты с пунктами назначения не в T[w], т.е., узлы с номерами в
ZN \[aw,bw) = [bw,aw).
[]
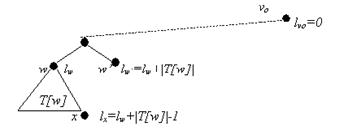
Рисунок 4.12 Префиксный обход дерева
Циклический интервал может быть представлен использование только 2 log N бит дающих начальный и конечный пункт. Так ка в этом приложении объединение разъединенных интервалов в объединении ZN должно хранится, достаточно logN бит на интервал. Хранится только начальная точка интервала для каждого канала; конечная точка эквивалентна начальной точке следующего интервала в том же узле. Начальная точка интервала приписанного каналу uw в узле u дается как
ì lw если w сын u,
auw = í
î lu+|T[u]| если w отец u
Положим что каналы узла u со степенью degu помечены a1,..., adeg u , где a1 < ,...,< adeg u , передающая процедура дана в Алгоритме 4.13. Метки каналов отображают ZN в сегменты degu , каждый соответствует одному каналу; см. Рисунок 4.14. Заметим что существует (не более чем) один интервал который не линейный. Если метка отсортированы в узле, соответствующая метка находится за О(log degu) шагов используя бинарный поиск. Индекс i вычисляется по модулю degu, т.e., adeg u+1 == a1.
(* пакет с адресом d был получен в узле u *)
if d = lu
then доставить пакет локально
else begin выбрать ai, т.ч. d Î [ai, ai+1) ;
послать пакет через канал с меткой ai
end
Алгоритм 4.13 Интервальная передача (для узла u).
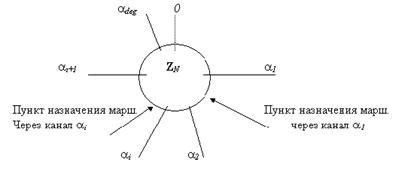
Рисунок 4.14 Часть ZN в узле.
Схема разметки деревьев маршрутизирует оптимально через деревья, потому что в дереве существует только один простой путь между каждыми двумя узлами. Схема может также использоваться если сеть не является деревом. Выбирается фиксированное дерево охвата T в сети, и схема применяется на этом дереве. Каналы не принадлежащие этому дереву никогда не используются; каждый помечен специальной меткой в таблице маршрутизации чтобы показать что нет пакетов проходящих через этот канал.
Сравним длины путей выбранное этой схемой с оптимальными путями, пусть dT(u, v) обозначает расстояние от u до v в T и dG(u, v) расстояние от u до v в G. Пусть DG обозначает диаметр G, определенный как максимум для любых u и v из dG(u, v).
Лемма 4.21 Нет общего ограничения пропорции между dT(u, v) и dG(u, v).Это имеет силу только в специальном случае измерения переходами путей.
Доказательство. Выберем G как кольцо из N узлов, и заметим что дерево охвата G получается удалением одного канала, скажем xy, из G. Теперь dG(x, y) = 1 и dT(x, y) = N-1,таким образом пропорция N—1. Пропорция может быть гораздо больше выбором большего кольца. []
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105


